DCG ...
Legacy 2014. 10. 15. 11:17원본 : http://freesearch.pe.kr/archives/1574
Discounted Cumulative Gain
DCG라는 metric은 기존의 precision, recall 기반의 검색엔진 평가 방법으로는 순위에 따른 차별점을 부과하기 힘들다는 판단에 따라 나온 방법이다.
이전에도 언급했지만 50% 이상의 검색 사용자가 검색 결과의 1,2 페이지 정도만 참고한다는 것은 precision, recall 만으로는 정확한 사용자 패턴에 기반한 성능평가를 하기 힘들다는 것을 알 수 있다.
Cumulative Gain
이는 그냥 n개의 검색 결과의 등급을 모두 합한 값이다. 관련성에 따라 3~0 사이의 값을 가진다고 하면 ideal CG와 현재 CG를 기반으로 절대적인 점수를 도출할 수도 있다.
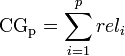
예를 들어 첫번째 결과에서 여섯번째 결과까지의 rel 등급이 3,3,2,0,1,2 라고 한다면 CG는 11의 값을 가지게 된다.
이 방법은 실제 검색 결과 위치에 따른 영향을 전혀 받지 않는 방법이다.
ideal CG는 어떻게 될까? 이는 18이 될 것이다.
Discounted Cumulative Gain
이는 실제 검색 결과 순서에 따른 패널티를 적용한 점수값을 도출한다.
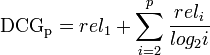
에디터가 산정한 rel점수에는 비례하지만 낮은 랭킹의 결과에 대해서 점진적인 패널티를 주기 위해 log 함수를 사용했다.
개인적인 생각으로 log 함수는 80:20 법칙에 가장 잘 맞는 함수라고 생각한다. 예를 들면 검색 결과 1,2위 사이의 간격은 정말 큰 차이지만 999위와 1000위 사이는 log의 값 차이이건 사용자가 느끼는 차이이건 그 차이가 거의 없다.
Normalizing DCG
위 DCG 점수는 현재 검색엔진의 결과의 상태를 보여준다. 그렇다면 가장 이상적인 검색엔진의 점수로 위 점수를 나누어 주면 정규화된 DCG가 나올 것이다.
![]()
현재 검색엔진의 순위대로 rel 등급이 3,3,2,0,1,2로 나왔다고 하면 DCG는 아래와 같이 계산될 수 있다.
그리고 이상적인 결과 순위는 3,3,2,2,1 이 될 것이다.
DCG = 3 + (3/log2 + 2/log3 + 0/log4 + 1/log5 + 2/log6) = 5.46
IDCG = 3 + (3/log2 + 2/log3 + 2/log4 + 1/log5) = 5.69
NDCG = 5.46 / 5.68 = 0.95
개인적으로 랭킹관련 평가를 할때 이 log함수를 많이 쓰고 있는데, log n값의 결과가 0이 되는 시기만 조심하면 랭킹관련 문제에서 아주 요긴하게 쓰일 수 있다.

